V-Lab @ ANDC

To verify the Law of Malus for plane polarised light.

Aim

To verify the Law of Malus for plane polarised light.

Apparatus

  1. A diode laser
  2. a polarizer-analyzer pair
  3. photo detector
  4. output measuring unit (micro ammeter)
  5. dial fitted to the polarizer and an optical bench .

Principle

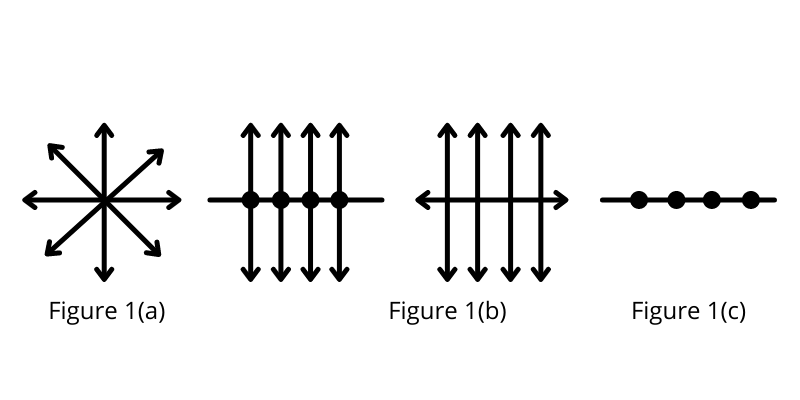
The light coming from the Sun, candle light, and light emitted by a bulb is an ordinary light and is known to be un-polarized. In an un-polarized light electric and magnetic field vectors vibrate in all possible directions perpendicular to each other and also perpendicular to the direction of propagation of light. Unpolarised light can be represented as shown in fig. 1(a). The unpolarised light can be considered to be composed of two linear orthogonal polarization states with complete incoherence. When unpolarized light is incident on an ideal polarizer, the intensity of the transmitted light is one-half of the incident light. Also if the polarizer is rotated w.r.t. incident light there is no change in the irradiance of the transmitted light i.e. its intensity remains half of the incident light.

Polarization-

Certain transparent materials such as Nicol, Tourmaline are capable of filtering and allowing light waves having vibrations in only one plane. Such materials are called Polaroids. This filtering is possible due the structure of the material that is having its cells arranged in a straight line manner only in one direction (parallel to the pass axis of polarizer) which is represented in fig. 1(b) & fig. 1(c). This phenomenon of filtering and producing light waves having vibrations confined to one particular direction is called polarization. Polarization is a property of a material by which light waves are filtered and made directional.


Malus's Law-

When light falls on a polarizer, the transmitted light gets polarized. The polarized light falling on another Polaroid, called analyzer, transmits light depending on the orientation of its axis with the polarizer. The intensity of light transmitted through the analyzer is given by Malus’ law. The law describes how the intensity of light transmitted by the analyzer varies with the angle that its plane of transmission makes with that of the polarizer. The law can be stated in words as follows:

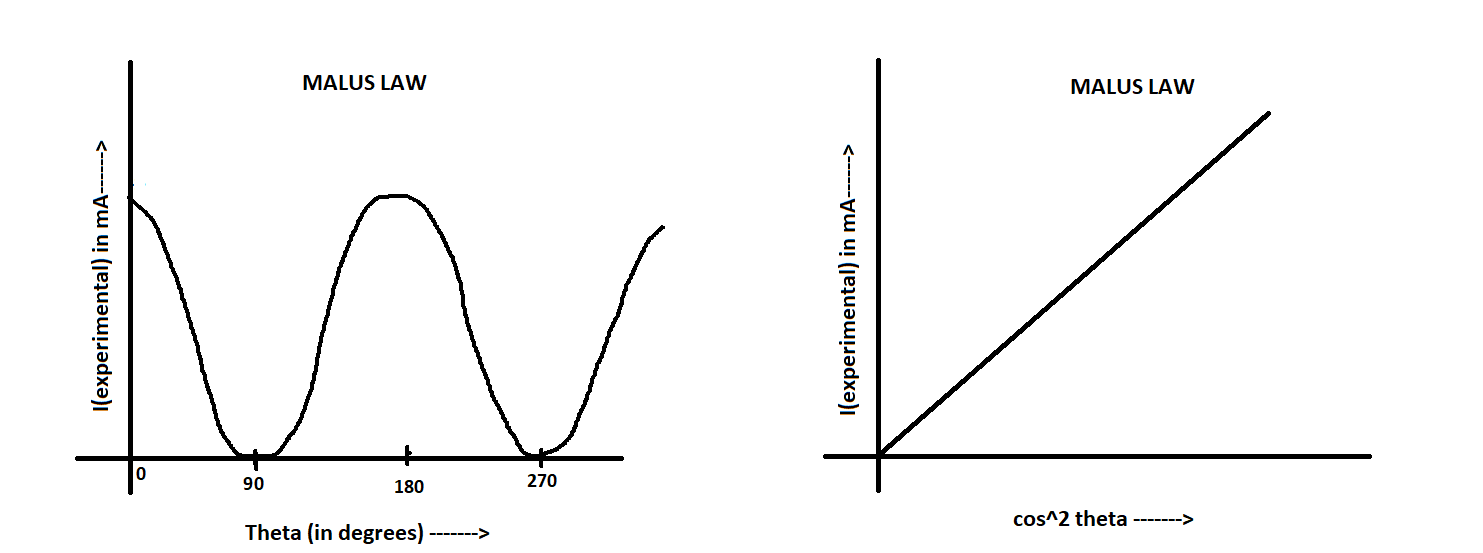
The intensity(I) of the transmitted light varies as the square of the cosine of the angle(φ) between the two planes of transmission. : 

I ∝ cos2 φ



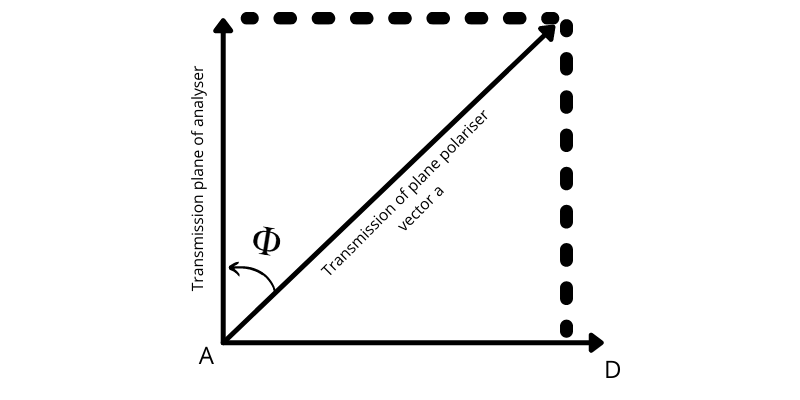
Let us suppose , that the angle between the planes of transmission of the polarizer and the analyser is φ at any instant (above graph). The electric vector AB = vector a in the plane polarised light emerging from the polariser may be resolved into two components AC(=a cos φ) and AD(=a sin φ) which are respectively along and perpendicular to the plane of transmission of the analyser. The perpendicular component is eliminated in the analyser while the parallel component is freely transmitted through it. Therefore, the intensity I of light that emerges from the analyser is given by 

 I ∝ a2 cos2 φ
I ∝ I0 cos2 φ 

 where I0is the intensity of the plane polarised light incident in the analyser. The
                intensity of the transmitted light is maximum when
φ = 90o
or when the polariser and analyser are crossed.
To verify this law, the light from the analyser is made to eneter a photovoltaic cell. The photocurrent produced is directly proportional to the intensity of light falling on the photovoltaic cell.The analyser(polaroid) is rotated in its own plane. The angle φ of rotation and the corresponding photocurrent I is noted. Hence if a graph is plotted between I and 
cos2φ,it would be a straight line, thus verifying Malus' Law.

Formula Used-

Intensity of the transmitted light is given by 

It2= At2=A02 cos2θ=I0 cos2θ

Where It is the intensity of the light transmitted through the analyzer;
I0 is the intensity of the incident plane polarized light and θ is the angle between the axis of polarizer and analyser.

Procedure

  1. Set up the laser, photodiode, the polarizer and analyser as shown in Figure 4 to test Malus's Law.
  2. Set angle of incidence at brewster's angle(nearly 56o).Make sure the polarizer and analyser are normal to the laser beam and that the beam passes through a “good” portion of the polarizers - look for minimal scattering, etc.
  3. When the laser is going through polarizer, analyser and then into a detector make sure polarizer and analyser transmission axes are parallel. That way you can work with an offset from θ o . To do this, keep the polarizer fixed and rotate the analyser until you observe a maximum in transmission. Note down maximum current Imax and angle as θo. At this point the pass axes of polarizer and analyser are parallel.
  4. Rotate the analyzer in 10o increments from φo to get 'θ' in a range 0 o to 360o . Take readings of the intensity at each angle. The intensity of light beam that passes through polarizer and analyser was measured by the light sensor. The rotary motion sensor measures the angle that was obtained from rotating the second analyzer relative to the first polarizer.
  5. In each case the current is noted and tabulated in Table-1.
  6. Plot a graph taking the current 'Iexpt' along Y-axis and angle of rotation of analyzer on the X-axis. From the graph the cosine nature of the curve is clearly evident, validating the Malus' law.
  7. Cos θ, Cos2θ, Itheo are calculated and presented in Table-1. Plot two more graphs showing the variation of Iexpt vs Cos2θ and Iexpt vs Itheo
  8. The slope of straight line in graph Iexpt vs Itheo is calculated. Slope ≈1

Animation

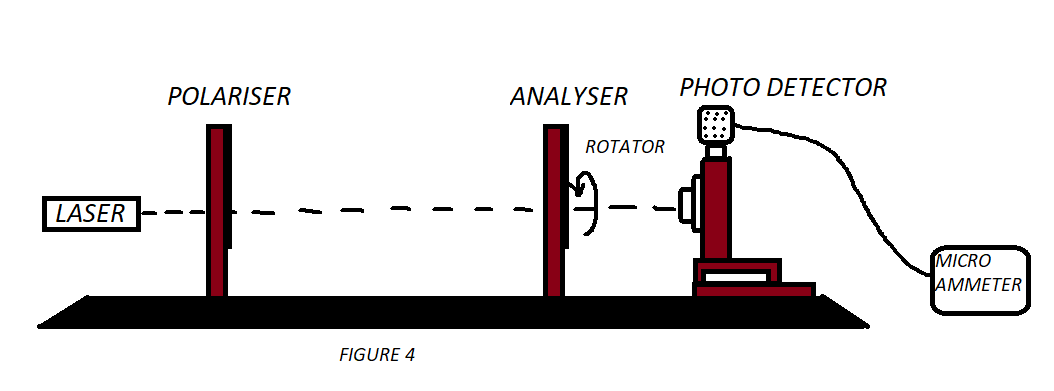
Animation of the experiment:--

Observation and calculation


Angle of Analyzer when current is maximum Φ o = ....... (degrees) 
 Maximum Current Imax= ......(μ amp)

Result & Discussion

Write at your own how the Malus law have been verified from your experimental data.

Precaution

  1. Analyzer and Polarizer should be at same horizontal level.
  2. Analyzer must be rotated by small angles (5o - 10o ). Changing values abruptly may cause errors.
  3. Experiment should be performed in dark room .
  4. Photo detector is a very sensitive device. It should be adjusted well (at appropriate height) to receive maximum current.

References

  1. Reference from Physics Practical - Geeta Sanon
  2. Wikipedia