The aim of this Virtual lab is to implement an adaptive search algorithm that automatically performs linear search for an unsorted list and binary search for sorted list.
The adaptive search algorithm combines the efficiency of binary search for sorted list and the simplicity of linear search for unsorted list. It determines the nature of the given sequence of elements by checking if it is sorted or unsorted. Based on the result, it applies the appropriate search algorithm. If the list is sorted, it performs binary search; otherwise, it resorts to linear search.
Search algorithms, such as linear search and binary search, are fundamental concepts with
various applications in computer science and real-world scenarios.
Its some applications
include:
- Database Systems: Search algorithms are widely used in database systems to efficiently retrieve information based on search queries.
- Information Retrieval: Search algorithms power search engines, helping users find relevant information on the web.
- Sorting and Searching in Libraries: These algorithms are used in libraries to organize and retrieve books efficiently.
- Network Routing: In networking, search algorithms play a crucial role in determining optimal routes for data transmission.
- Game Development: Search algorithms are utilized in games to find paths, search for objects, or make decisions based on game states.
The procedure for implementing the adaptive search algorithm can be summarized as follows:
- Input the desired list.
- Take the target element to be searched in the input list from the user.
- Check if the list is sorted or unsorted:
- If the list is sorted, apply the binary search algorithm.
- If the list is unsorted, apply the linear search algorithm.
- If the binary search algorithm is applied:
- Initialize the search range, which initially includes the entire sorted list.
- Divide the search range in half and compare the target element with the middle element of the range.
- Adjust the search range iteratively by reducing it by half with each iteration until the target element is found or the search range is empty.
- If the target element is found, return the index of the element. If the search range is empty, conclude that the element is not present.
- If the linear search algorithm is applied:
- Iterate sequentially in the unsorted list by comparing with the target element.
- If a match is found, return the index of the element. If the entire list is traversed without finding a match, conclude that the element is not present.
Example
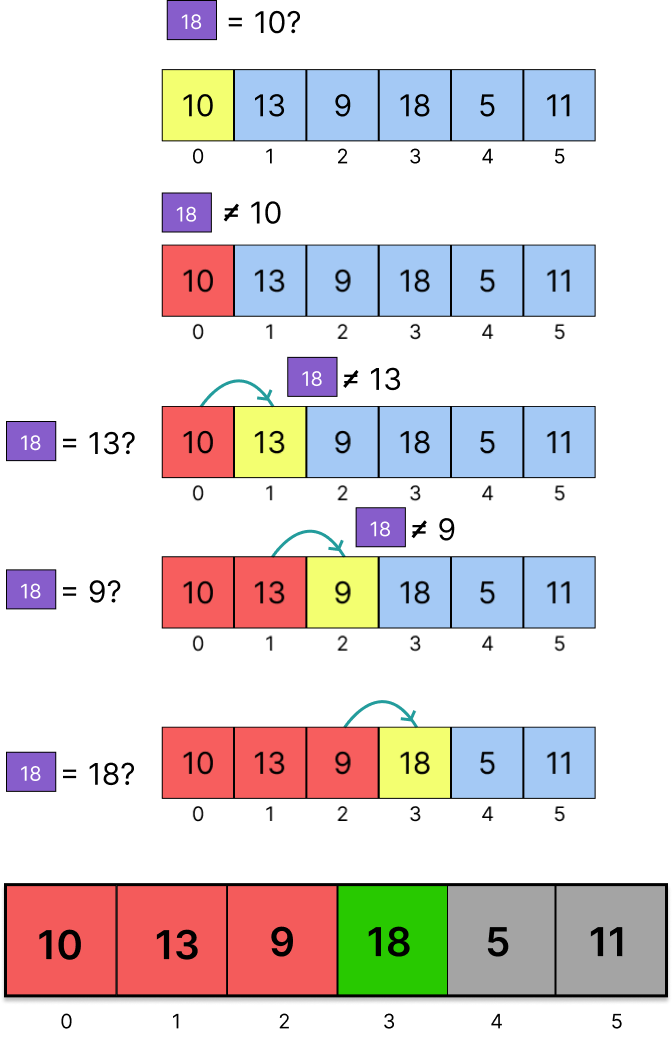
If the list is unsorted it performs Linear Search:
Suppose that the input list is [10, 13, 9, 18, 5, 11] and the target element to be found in the
list is 18.
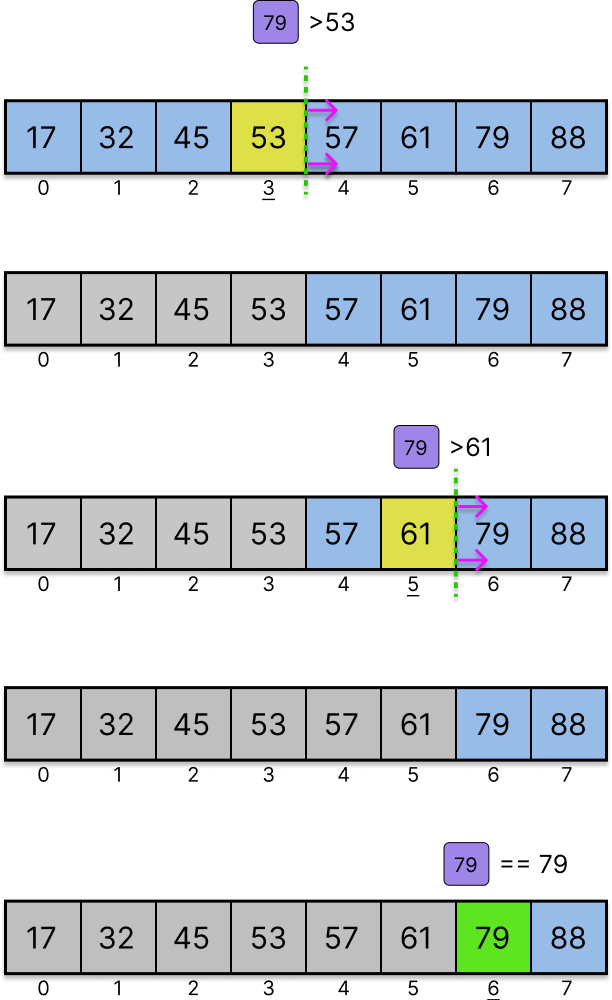
If the list is sorted then perform Binary Search:
Suppose that the input list is [17, 32, 45, 53, 57, 61, 79, 88]. We have to find the element
79 in the list.
- Mid index: (0 + 7) / 2 = 3
- Since 53 is less than 79, search the right half.
- Mid index: (4 + 7) / 2 = 5
- Since 61 is less than 79, search the right half of the remaining elements.
- Mid index: (6 + 7) / 2 = 6
- Value equals 79, search successful. Index 6 is the position of 79 in the sorted list.
Adaptive Search Simulator
Enter a list of numbers and a target element. The simulator automatically decides whether to use Linear Search (if the list is unsorted) or Binary Search (if the list is sorted). Observe step-by-step how the algorithm narrows down or scans through the list.
⚡ Pro tip: Try entering both sorted and unsorted arrays to see the difference!
Array Visualization
Step-by-Step Execution
Example programs
// C++
#include < iostream >
using namespace std;
int linearSearch(const int* arr, int size, int target) {
for (int i = 0; i < size; ++i) {
if (arr[i] == target)
return i; // Found the target
}
return -1; // Target not found
}
int binarySearch(const int* arr, int size, int target) {
int left = 0;
int right = size - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target)
return mid; // Found the target
if (arr[mid] < target)
left = mid + 1;
else
right = mid - 1;
}
return -1; // Target not found
}
struct Search{
/*
Defines a structure named 'Search' that is used to represent search results or items.
The 'Search' structure has two members:
'index' (integer): Represents the index or position of a search result or item.
'sorted' (integer): Indicates whether the search result or item is sorted.
This structure can be utilized to organize and store information
related to search operations, such as maintaining the index and sorted
status of search results in a list.
*/
int index;
int sorted;
};
Search adaptiveSearch(const int* arr, int size, int target){
Search searchResult;
searchResult.sorted =0;
searchResult.index =-1;
// Check if the list is sorted
bool isSorted = true;
for (int i = 1; i < size; ++i) {
if (arr[i] < arr[i - 1]) {
isSorted = false;
break;
}
}
if (isSorted){
searchResult.index = binarySearch(arr, size, target);
searchResult.sorted = 1;
return searchResult;}
else{
searchResult.index = linearSearch(arr, size, target);
searchResult.sorted = 0;
return searchResult;}
}
int main() {
int sizeA,target,value;//sizeB,
cin>>sizeA;//sizeB;
int list[sizeA] ;
cout<<"Enter your list:\n";
for (int i = 0;i< sizeA;i++){
cin>>value;
list[i]=value; }
cout<<"Enter the target: "; cin>>target;
Search result = adaptiveSearch(list, sizeof(list) / sizeof(list[0]), target);
if(result.sorted){
if (result.index != -1){
cout << "Binary search: Found at index " << result.index << endl;}
else{
cout << "Binary search: Not found" << endl;}
}
else{
if (result.index != -1){
cout << "Linear search: Found at index " << result.index << endl;}
else{
cout << "Linear search: Not found" << endl;}
}
}
# Python
def linear_search(arr, target):
"""
Performs linear search on the given list to find the target element.
Args:
arr (list): The list to be searched.
target: The element to be found in the list.
Returns:
int: The index of the target element if found, -1 otherwise.
"""
for i in range(len(arr)):
if arr[i] == target:
return i # Target element found, return the index
return -1 # Target element not found
def binary_search(arr, target):
"""
Performs a binary search on the given sorted list to find the target element.
Args:
arr (list): The sorted list to be searched.
target: The element to be found in the list.
Returns:
int: The index of the target element if found, -1 otherwise.
"""
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
def main():
# Take input from the user
arr = input("Enter the list (space-separated integers): ").split()
arr = [int(x) for x in arr]
target = int(input("Enter the target element: "))
# Determine if the list is sorted
is_sorted = sorted(arr) == arr
# Perform the appropriate search
if is_sorted:
print("Sorted list given.\nPerforming Binary Search.")
index = binary_search(arr, target)
if index == -1:
print(f"The target {target} is not found in the sorted list.")
else:
print(f"The target {target} is found at index {index} in the sorted list.")
else:
print("Unsorted list found.\nPerforming Linear Search.")
index = linear_search(arr, target)
if index == -1:
print(f"The target {target} is not found in the unsorted list.")
else:
print(f"The target {target} is found at index {index} in the unsorted list.")
if __name__ == "__main__":
main()
The adaptive search algorithm will apply appropriate searching algorithm (linear/binary) as per the ordering of the elements in the input list. It will return the index of the target element if it is found in the list or -1 if the element is not present.
Intructions
- Quiz contains 8 multiple-choice questions. Read each question carefully before answering.
- Select the correct option(s).
- Click Next to move to the following question.
- At the end, you can view your quiz report and retake the quiz if needed.
- Cormen, T. H., Leiserson, C. E., Rivest, R. L., Stein, C. (2022). Introduction to Algorithms, Fourth Edition. United Kingdom: MIT Press.
- Bhargava, A. (2016). Grokking Algorithms: An Illustrated Guide for Programmers and Other Curious People. United States: Manning.
Students
- Mayank Kumar - B. Sc. (H) Computer Science, 2nd yr (2023-24)
- Nishant Pratap Singh - B. Sc. (H) Computer Science, 2nd yr (2023-24)
Mentors
- Prof. Sharanjit Kaur
- Ms. Gunjan Rani
- Ms. Nishu Singh
Tools Used
- Vanilla HTML, CSS, JS - for creating the web page
- Figma - for designing figures and UI mockups
